Aproximación de Pi en La Biblia Publicado por ^DiAmOnD^ el 27 de Febrero de 2008 TOMADO DE GAUSSIANOS

Javier Diez

21/07/2016

Quisiera señalar 2 hechos fáciles de verificar que contradicen la idea de que la Biblia dice que pi = 3. Conozco más, pero con estos dos basta:

1) en el mismo versículo 1 Reyes 7:23 hay una “falta de ortografía” en el original hebreo, la cual ha sido perpetuada por la tradición judía porque se considera que estos “aparentes errores” muchas veces pueden contener un mensaje cifrado. El error consiste en que la palabra que se traduce al español por “línea” en ese versículo está mal escrita en hebreo, y realmente lo que dice es algo que habría que traducir por “esperanza”. El error se debe a que línea es una palabra de 2 letras (KUF-VAV) pero está escrita con 3 letras (KUF-VAV-HEH). Ahora bien, el valor de Gematría de la palabra bien escrita es 106 (KUF = 100, VAV = 6), y el de la palabra mal escrita es 111 (HEH = 5). Y alguien descubrió hace relativamente poco tiempo, pero a estas alturas es un hecho bien conocido, que ese “error ortográfico” es una forma cifrada de corregir el otro aparente error del versículo (el que dice que pi = 3). La observación es simple, y cada uno decide si es o no una casualidad. Pero si se multiplica 3 * 111/106, lo que se obtiene es 3,1415… el “error ortográfico” corrige al “error aritmético” del versículo, y viceversa. Y cabe preguntarse, si no era mediante un error ortográfico, ¿de qué otra manera podía guardarse para la posteridad un ajuste numérico en una lengua que sólo manejaba números enteros?

2) Más interesante es esto: el valor pi = 3,1415 se encuentra codificado en Génesis 1:1, y el valor e = 2,7183 en Juan 1:1. No se trata de 2 versículos al azar de la Biblia, se trata del primer versículo del Antiguo Testamento (Génesis 1:1) y del primer versículo del único Evangelio que inicia su relato en el momento de la Creación del mundo, lo cual permite considerarlo en muchos sentidos como el primer versículo del Nuevo Testamento. Son los dos versículos “en el principio” de toda la Biblia, y comienzan con esas palabras. El nivel de precisión para pi = 3,1415 en Génesis 1:1 es de 1 parte en 200.000, y el de e = 2,7183 en Juan 1:1 es de 1 parte en 300.000, por lo cual el evento combinado de que ambos ocurrieran tiene una chance en 60.000 millones! Podrías apostar a que es casualidad, pero llevarías todas las de perder!

A continuación les muestro brevemente cómo se encuentran esos números en dichos versículos. Simplemente, considerando el valor de Gematría de cada letra y de cada palabra del versículo respectivo (esto puede hacerse con cualquiera de esos dos versículos, o con cualquier otro versículo, si quieren buscar más números), se hace la siguiente cuenta:

cantidad de letras * producto del valor de todas las letras
——————————————————————————–
cantidad de palabras * producto del valor de todas las palabras

Si se hace esta cuenta para las letras y palabras de Génesis 1:1, se obtiene 3,1415…, es decir pi.
Y si se hace la misma cuenta para las letras y palabras de Juan 1:1, se obtiene 2,7183…, es decir e.

Si quieren ver una descripción paso a paso de cómo llevar a cabo estas cuentas (letra por letra y palabra por palabra), pueden verlo en:
– pi en Génesis 1:1: http://daniel1210.com/epi/04/
– e en Juan 1:1: http://daniel1210.com/epi/05/

Pueden chequear las tablas de Gematría de las lenguas hebrea y griega aquí:
– para el hebreo: http://daniel1210.com/epi/A1/
– para el griego: http://daniel1210.com/epi/A2/

(o bien en wikipedia, “Gematría hebrea” y “Gematría griega”)

CURIOSIDAD TOMADA DE GAUSSIANOS COMO DETECTAR NUMEROS PRIMOS CON EL TRIANGULO DE PASCAL

Publicado por ^DiAmOnD^ el 28 de Febrero de 2017 en Curiosidades, Números primos, Otras constantes, Pi | 0 comentarios

En el conocidísimo triángulo de Pascal pueden encontrarse multitud de tesoros matemáticos (recopilé unos cuantos aquí). Algunos de ellos son fáciles de localizar, pero otros están algo más escondidos. Hoy hablaremos de cómo encontrar la sucesión de Fibonacci y los ¡¡números primos!! en este interesante triángulo numérico.

¿Que no sabes qué es el triángulo de Pascal? Pues aquí lo tienes. Cada fila tiene unos a izquierda y derecha, y cada posición intermedia se calcula sumando los dos números que tiene justo encima:

En este blog ya hemos tratado algunos de estos tesoros de los que hablábamos al principio. Hemos visto su relación con los números de Catalan; vimos cómo encontrar el número e y el número Pique aparecen relacionados con el número 89 y el número 109; presentamos una interesante conjetura sobre sus elementos y también enseñamos una forma de relacionar el triángulo de Pascal y la sucesión de Fibonacci…

…y por ahí vamos a comenzar. La relación que vimos en aquella entrada es la que se puede ver en la siguiente imagen:

Pues hace poco me encontré una anotación en Futility Closet en la que daban otra forma de encontrar los números de Fibonacci en el triángulo de Pascal. La cuestión es como sigue:

Coloca la primera fila, el 1, y luego coloca el resto de filas desplazadas una posición hacia la derecha respecto de la fila justo anterior. Si ahora sumamos las columnas que nos quedan, obtenemos los números de la sucesión de Fibonacci:

Precioso, ¿verdad? Pues sí…pero si le echamos un nuevo vistazo a la tabla con las filas desplazadas y a la imagen que puse antes sobre los números de Fibonacci…¿lo veis? Exacto: son la misma cosa. Por lo que, por ahora, esto no aporta mucho más que lo que ya teníamos.

La cosa es que, al final de aquel post de Futility Closet, aparecía un enlace a otro post del mismo blog en el que se hablaba de números primos y el triángulo de Pascal (concretamente éste). Y de ello vamos a hablar ahora.

Lo que nos enseñaba Greg Ross en aquella entrada era una forma de detectar números primos usando los elementos del triángulo de Pascal de una manera cuando menos curiosa, y vamos a explicarla. Creamos una tabla en la que colocamos los enteros mayores o iguales que cero en la primera fila y en la primera columna, y dentro colocamos las filas del triángulo de Pascal de manera que la fila  comience en la columna 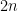. Es decir, la fila 0 comenzará en la fila 2·0=0, la fila 1 en la columna 2·1=2, la fila 2 en la columna 2·2=4, y así sucesivamente. Las 8 primeras filas quedarían de la siguiente forma:

¿Cómo podemos ahora detectar números primos? Pues así:

Un número de la fila superior es primo si cada uno de los elementos de su columna es divisible por su correspondiente número de fila.

Podéis ver que este resultado se cumple en la tabla que hemos visto justo antes. Se puede ver que los números primos, recuadrados en rojo, cumplen que todos los elementos de su columna son divisibles entre los de la fila a la que pertenecen:

Este curioso resultado data de 1971 y fue demostrado por Henry B. Mann y Daniel Shanks. Podéis ver la demostración (bastante corta y sencilla) en A necessary and sufficient condition for primality, and its source.

---

Esta entrada participa en la Edición 8.1 del Carnaval de Matemáticas, que en esta ocasión organiza nuestro querido amigo Tito Eliatron.

Autor: ^DiAmOnD^

Miguel Ángel Morales Medina. Licenciado en Matemáticas y autor de Gaussianos y de El Aleph. Puedes seguirme en Twitter o indicar que te gusta mi página de Facebook.